SOLUCIONES_MEDIATRIZ_EJERCICIO CAJA DE ESCALESRAS

Trazamos el segmento que une los puntos I y J

Hallamos la mediatriz de dicho segmento

Se trazan dos arcos de igual radio arbitrario desde los puntos I y J (radio > IJ/2). Los dos arcos se cortan en dos puntos L y K que pertenecen a la mediatriz, puesto que cumplen la condición de equidistar de los extremos del segmento.

Finalmente se traza la mediatriz, recta que contiene los puntos L y K

Repetiríamos la misma operacion con las otras dos plantas para acabar de solucionar el problema.

MEDIATRIZ_EJERCICIO CAJA DE ESCALERAS

Para practicar el concepto de mediatriz resuelve el siguiente ejercicio:

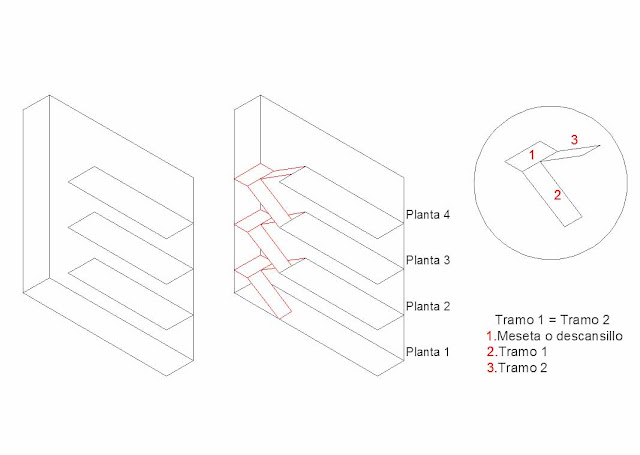
Un edificio de viviendas tiene 4 plantas. Para acceder a cada una de las plantas, además del ascensor, hay una escalera que recorre todo el edificio.

La escalera es de dos tramos por planta y la meseta o descansillo de la misma siempre se encuentra en la mitad de cada planta. Por tanto, los dos tramos de escalera de una misma planta son iguales.

Sabiendo todo lo anterior, dibuja sobre el esquema dado y a la altura correspondiente la recta en la que se encuentra la meseta de la escalera de cada planta.

Unos esquemas para que te situes mejor:

Y ahora el gráfico sobre el que debes dibujar la solución:

MEDIATRIZ

En esta entrada aprenderás:

1. Qué es una mediatriz de un segmento.
2. Cómo se realiza la construcción gráfica de una mediatriz.
3.Aplicaciones de la mediatriz en la geometría.

MEDIATRIZ DE UN SEGMENTO AB:

Es la recta (r) perpendicular a dicho segmento que pasa por su punto medio M ( M= AB/2).

Además la mediatriz de un segmento cumple que: cualquier punto (P) de ella equidista de los extremos del segmento A y B, es decir, AP=BP.

CONSTRUCCIÓN GRÁFICA DE LA MEDIATRIZ:

1-Se trazan dos arcos de igual radio arbitratio desde el punto A y B. El radio de dichos arcos siempre debe ser mayor que la mitad de la longitud del segmento.
2-Los dos arcos se cortan en dos puntos C y D que pertenecen a la mediatriz, puesto que cumplen la condición de equidistar de los extremos del segmento.

APLICACIONES DE LA MEDIATRIZ EN GEOMETRÍA:

GEOMETRIA DINÁMICA_TEOREMA DE PITÁGORAS

Con esta geometría dinámica entenderás mejor el Teorema de Pitágoras. Arrastra el punto B con el ratón y comproborás que la hipotenusa al cuadrado siempre es igual a la suma de los catetos al cuadrado.

SOLUCIONES_TEOREMAS_EJERCICIO FOTO-LIENZO

El problema se podría resolver graficamente gracias al Teorema de Thales. Recuerda que una de las aplicaciones directas del Teorema de Thales son las escalas.

Dicho teorema se enuncia de la siguiente manera: Si cortamos dos rectas cualesquiera por varias rectas paralelas, los segmentos correspondientes en ambas son proporcionales, es decir, se corresponden en la igualdad, en la suma y en la resta.

Aplicando Thales a nuestro ejercicio, para resolverlo, basta con:

Para hallar las siete columnas del lienzo: colocaremos foto y lienzo de forma que el lado largo de la foto y el lado largo del lienzo formen dos rectas cualesquiera.  Despúes trazamos la recta que une los extremos libres del lienzo y la foto (P3).

Para hallar las cinco filas del lienzo: colocaremos foto y lienzo de forma que el lado corto de la foto y el lado corto del lienzo formen dos rectas cualesquiera. Despúes trazamos la recta que une los extremos libres del lienzo y la foto (P2).

Ahora solo nos falta trazar paralelas a las rectas P2 y P3 que pasen por los puntos que definen las columnas y filas de la foto:

¡Ya está resuelto!, es fácil ¿verdad?

TEOREMAS_THALES_EJERCICIO FOTO-LIENZO

Después de que te hayas familiarizado con los teoremas de Pitágoras y Thales, te propongo el siguiente ejercicio para que puedas practicar los conceptos aprendidos:

Paula se ha apuntado a una academia de dibujo para aprender la técnica de dibujo al óleo. El profesor le ha pedido que lleve una foto de algo que le guste para después copiarlo en un lienzo. Una vez en clase, le indican que tiene que dividir la foto y el lienzo en 7 columnas y 5 filas, de esa forma, cuando vaya completando el lienzo tendrá una referencia de si está guardando bien o no la proporción. Si las columnas y las filas de la foto son las abajo dibujadas, calcula graficamente como deberían ser las divisiones del lienzo.
SOLUCIÓN: