Determina la figura A1B1C1D1, inversa de la ABCD dada, en una inversión de centro
O que convierte el punto A en A1.
martes, 29 de marzo de 2016
SOLUCIONES_INVERSIÓN_EJERCICIO_1
Recordamos el enunciado:
Determina la figura A1B1C1D1, inversa de la ABCD dada, en una inversión de centro
O que convierte el punto A en A1.
Sabemos que la inversión es una transformación en la que se
cumple que:
1- La transformación
es con centro: Un punto y su inverso están alineados con el centro de
inversión (O).
2- La relación entre las posiciones relativas de cada punto
y su transformado respecto del centro de inversión se basan en el concepto de
potencia. El producto de la distancia de
un punto al centro de inversión por la distancia de su inverso al centro de inversión
es constante (K) y se llama potencia de inversión. Por ello se cumple que:
OA*OA1 = OB*OB1 = OC*OC1=OD*OD1= OT*OT=K
Puesto que A, C y D están a la misma distancia del polo, la
única manera de que se cumplan las dos condiciones citadas es que A1, C1, D1 se encuentren sobre una circunferencia de centro O y radio el
determinado por el valor de la potencia de inversión.
Puesto que en el
enunciado nos facilitan A1,
punto inverso de A, los puntos C1,
D1 estarán sobre la
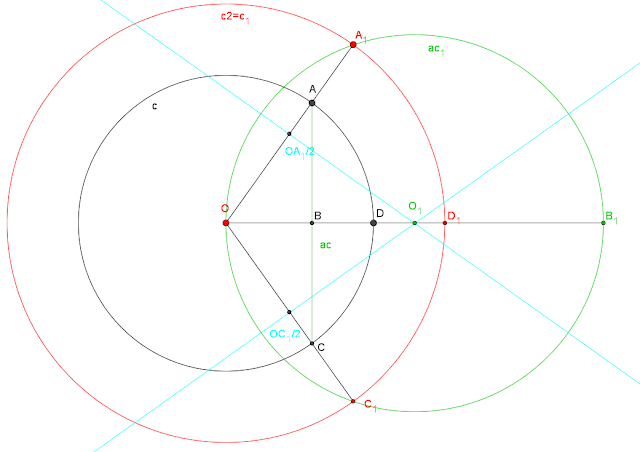
circunferencia de centro O y radio A1, que llamaremos c2. Por ser una transformación con centro, los
puntos inversos C1, D1 se encuentran concretamente
donde la recta que une cada punto con el centro de inversión intersecciona con la
circunferencia c2, como muestra la siguiente figura:
Ahora nos proponemos invertir la circunferencia c, sabemos
que:
La inversión de una
circunferencia que no pasa por el centro de inversión es otra circunferencia
que tampoco pasa por O y que es homóloga a la primera.
Puesto que los puntos A, C y D pertenecen a la
circunferencia c sus puntos inversos A1, C1, D1 pertenecerán a la
circunferencia invertida c1.
Tenemos tres puntos de la circunferencia inversa buscada, luego ya podemos
dibujarla. Observamos que la circunferencia buscada coincide con C2. Lo cual nos permite
generalizar y enunciar la siguiente conclusión:
La inversión de una
circunferencia cuyo centro y centro de inversión coinciden es otra
circunferencia concéntrica a la misma.
Hallamos ahora la inversa de la recta que pasa por los
puntos A y C, sabemos que:
La inversión de una
recta que no pasa por el centro de inversión es una circunferencia que pasa por
el centro de inversión y a la que llamaremos ac1. Puesto que ya conocemos tres puntos de dicha
circunferencia O, A1y C1 ya podemos dibujarla. Basta
con hallar las mediatrices de los segmentos O-A1 y O-C1
y donde se corten se encontrará el centro O1 de dicha circunferencia.
Finalmente hallamos el punto B1 inverso del punto B. Deberá pertenecer a la
circunferencia ac1 y
estar alineado con los puntos O y B, luego ya podemos dibujarlo.
Hemos acabado nuestro ejercicio, la figura inversa buscada
es la definida por los puntos A1,
B1, C1 y D1 y las circunferencias c1 y ac1, o lo que es lo mismo, la figura resultante de la diferencia de
las circunferencias c1 y
ac1.
Suscribirse a:
Comentarios (Atom)